i’m going to calculate this using the binomial distribution, where n = number of button presses, and p = 0.99. so, if we let X be a random variable that follows that binomial distribution B(n, 0.99), then X corresponds to how many times we win money after pressing the button n times. (e.g., if we “only” get $10,000,000 after n button presses, then X = 1.)
in this setup, the probability of getting a billion dollars is given by
(this is basically just summing up all scenarios in which we get the money outcome at least 100 times.)
to calculate the chance of getting a billion dollars and becoming a woman, notice that we are guaranteed to be a woman so long as we hit the button fewer than n times. so, the probability of getting a billion dollars and becoming a woman is given by
to answer your questions, we just need to find the smallest value of n that makes both of the above equations greater than or equal to 0.90. there are probably some clever math tricks that could be utilized to do this, but i just wrote some python code to do it. the values are:
minimum number of presses for a 90% chance of getting a billion dollars: 102 button presses.
minimum number of presses for a 90% chance of getting a billion dollars and becoming a woman: 230 button presses.
37% chance to make a billion dollars.
63% chance to make less than a billion dollars and turn into a woman.
Nuh uh 1% times 100 is 100% idiot
/s obviously
How many times do I have to press it to get a 90% chance of having a billion dollars? What about a 90% chance of both?
Asking for a me who took statistics too long ago and is too sick to sit down and work it out.
okay so bear with me here.
i’m going to calculate this using the binomial distribution, where n = number of button presses, and p = 0.99. so, if we let X be a random variable that follows that binomial distribution B(n, 0.99), then X corresponds to how many times we win money after pressing the button n times. (e.g., if we “only” get $10,000,000 after n button presses, then X = 1.)
in this setup, the probability of getting a billion dollars is given by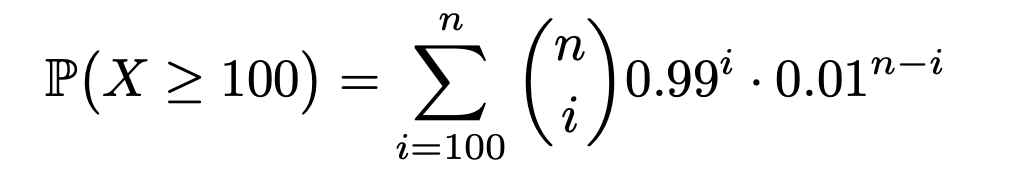
(this is basically just summing up all scenarios in which we get the money outcome at least 100 times.)
to calculate the chance of getting a billion dollars and becoming a woman, notice that we are guaranteed to be a woman so long as we hit the button fewer than n times. so, the probability of getting a billion dollars and becoming a woman is given by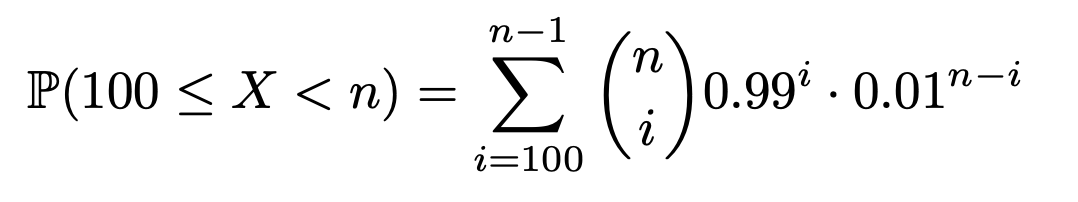
to answer your questions, we just need to find the smallest value of n that makes both of the above equations greater than or equal to 0.90. there are probably some clever math tricks that could be utilized to do this, but i just wrote some python code to do it. the values are:
minimum number of presses for a 90% chance of getting a billion dollars: 102 button presses.
minimum number of presses for a 90% chance of getting a billion dollars and becoming a woman: 230 button presses.
Presses the button 230 times