Remind me with party is the party of “family values” again?
Uh.
What the hell happened to Alaska, Hawaii, Illinois, Kansas, Michigan, Nevada, New Hampshire, New Mexico, Ohio, Pennsylvania, Vermont, Virginia, and Wisconsin? Did they all fall into the ocean or something?
The graphic is per the New York Times and the Bipartisan Policy Center,
I am assuming the states that aren’t listed have neither extreme abortion bans, nor guaranteed paid family leave.
I like how the District of Columbia is referred to as a state.
This isn’t meant to be funny, DC deserves statehood.
Caring about Kids DOESN’T mean making sure they grow up in a Loving Home! If it DID then we wouldn’t have School Shooters and I would NEVER get to Pretend I like the Constitution!
deleted by creator
The absence of overlap highlights the issue.
States with abortion bans are not helping families who want kids with guaranteed family leave.
deleted by creator
The overlap is an empty set. It is still a set, but it has no elements in it
Eh, in this instance I disagree.
By showing the overlap and not including any states in the overlap, it draws extra attention to the point of diagram which is that there isn’t any overlap.
deleted by creator
A Venn diagram does not imply that the intersection of the two sets is nonempty. It is merely a visual aid to illustrate the contents of two sets, and the center part is the intersection of those sets, which can be the empty set if the sets are disjoint (as they are in this context). The use of a Venn diagram is often used to show similarities and differences between two sets, but in this case the lack of any shared elements is actually the focal point of the diagram, used to illustrate a point. Showing disjoint sets disconnected from one another doesn’t send merely as powerful of a message as showing disjoint sets in a Venn diagram, as the Venn diagram highlights the fact that they have no common elements. The reader is immediately drawn to the center of a Venn diagram when one is shown, and given that the center has no labels, it is a quick and effective way to illustrate that the sets are disjoint, especially when the reader notices how many labels exist in either set.
The essential point here is that the use of a Venn diagram does not imply shared members, it merely implies that sets are being compared.
Literally it’s a thing:
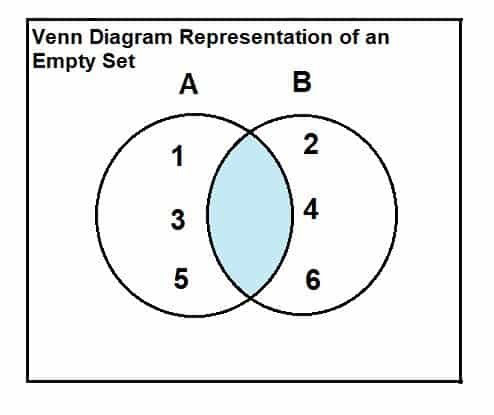
A = {1, 3, 5}
B = {2, 4, 6}
A ∩ B = ∅
If two sets have no elements in common, the regions do not overlap.
You seem to have skipped over the context in the Wikipedia page. That statement is true for an Euler diagram, not a Venn diagram. The next paragraph actually says outright that this is not the case for Venn diagrams. Here is that paragraph;
A Venn diagram, in contrast, is a graphical representation of n sets in which the n loops divide the plane into 2^n zones such that for each way of selecting some of the n sets (possibly all or none), there is a zone for the elements that belong to all the selected sets and none of the others. For example, if the sets are A, B, and C, there should be a zone for the elements that are inside A and C and outside B (even if such elements do not exist).
Note the “(even if such elements do not exist)”.
You can find the Wikipedia page on Venn diagrams here, which further illustrates this point (I have linked to the section that starts off by detailing how all relationships between sets are shown in Venn diagrams, even if they are empty, which is in contrast to Euler diagrams)




